 \{\mathop{\mathop{…}},(36,2),(40,5),(44,8),(48,11),(52,14),(56,17),(60,20),\mathop{\mathop{…}}\}.
\{\mathop{\mathop{…}},(36,2),(40,5),(44,8),(48,11),(52,14),(56,17),(60,20),\mathop{\mathop{…}}\}.
Notes also available as PDF.
In a few weeks, we will examine linear equations ax + by = c over real numbers. But many every-day applications require integer solutions. We can use the Euclidean algorithm to find one integer solution to ax + by = c or prove there are none. Then we can use the computed gcd to walk along the line to all integer solutions.
Some solvable problems:
A 98 pound box contains 5 pound bags of sugar and 12 pound sacks of oranges. How many of each are in the box?
Or:
Say you need a digital image in a 4 : 3 aspect ratio (x : y) that includes a 50 pixel border along each side. What sizes are possible for the inner image?
Consider the latter problem. Rephrasing algebraically,
We start by solving
|
3x - 4y = 1
|
and then multiplying the base solutions by 100. This case has one easy solution, x = -1 and y = -1, with 3 ⋅-1 - 4 ⋅-1 = -3 + 4 = 1. Another solution is x = 3 and y = 2.
In fact, there are infintely many solutions to 3x - 4y = 1 given by
for any integer t. You can substitute these expressions into 3x - 4y to verify the result. Scaling the right-hand side by 100, solutions to 3x - 4y = 100 are given by
For x > 0 and y > 0, we need t > 33. So the first positive solutions are given by t = 34,35,\mathop{\mathop{…}} and are
|
(x,y)  \{\mathop{\mathop{…}},(36,2),(40,5),(44,8),(48,11),(52,14),(56,17),(60,20),\mathop{\mathop{…}}\}. \{\mathop{\mathop{…}},(36,2),(40,5),(44,8),(48,11),(52,14),(56,17),(60,20),\mathop{\mathop{…}}\}.
|
Say we need to solve ax + by = c for integers a, b, and c to find integer solutions x and y. In general, equations over integers are called Diophantine equations after Diophantus of Alexandria (approx. 200AD-290AD). He was the first known to study these equations using algebra. The form ax + b = c describes linear Diophantine equations.
Let d = (a,b). Then, as before, d\mathrel{∣}ax + by for all integers x and y. So d\mathrel{∣}c for any solutions to exist. If d ∤ c, then there are no integer solutions. If a and b are relatively prime, then (a,b) = 1 and solutions exist for any integer c.
Consider solving ax + by = d. Because d\mathrel{∣}c, we can multiply solutions to ax + by = d by c∕d to obtain solutions of ax + by = c. To solve ax + by = d we work backwards after using the Euclidean algorithm to compute d = (a,b).
Say the algorithm required k steps, so d = {r}_{k-1}. Working backward one step,
So d = {r}_{k-1} = i ⋅ {r}_{k-3} + j ⋅ {r}_{k-4} where i and j are integers. Continuing, the gcd d can be expressed as an integer combination of each pair of remainders.
Returning to the example of (77,53), we found
Working from the second to the last,
To solve 53x + 77y = 22, we start with 53 ⋅ 16 + 77 ⋅ (-1) = 1. Multiplying by 22,
|
53 ⋅ (16 ⋅ 22) + 77 ⋅ (-1 ⋅ 22) = 22,
|
and x = 352, y = -22 is one solution.
But if there is one solution, there are infinitely many! Remember that d = (a,b), so a∕d and b∕d are integers. Given one solution x = {x}_{0} and y = {y}_{0}, try substituting x = {x}_{0} + t ⋅ (b∕d) and y = {y}_{0} - t ⋅ (a∕d) for any integer t. Then
Actually, all integer solutions to ax + by = c are of the form
|
x = {x}_{0} + t ⋅ (b∕d),\quad \text{and}\quad y = {y}_{0} - t ⋅ (a∕d),
|
where t is any integer, d = (a,b), and {x}_{0} and {y}_{0} are a solution pair.
Another example, consider solving 12x + 25y = 331. First we apply the Euclidian algorithm to compute (12,25) = 1:
Substituting back,
So we can generate any solution to 12x + 25y = 331 with the equations
Using these, we can find a “smaller” solution. Try making x non-negative with
Substituting t = 27,
|
x = 13,\quad \text{and}\quad y = 7.
|
Interestingly enough, this must be the only non-negative solution. A larger t will force y negative, and a smaller t forces x negative. But the solution for t = 26 is still “small”,
|
x = -12,\quad \text{and}\quad y = 19.
|
Our other posed problem:
A 98 pound box contains 5 pound bags of sugar and 12 pound sacks of oranges. How many of each are in the box?
So we need to solve 5x + 12y = 98, and start with 5x + 12y = 1.
Computing (12,5),
So (12,5) = 1. Because 1\mathrel{∣}98, there are infinitely many integer solutions. We need to find the non-negative solutions from those.
For a base solution,
So {x}_{0} = 5 and {y}_{0} = -2 solve 5x + 12y = 1. Multiplying by 98,
|
{x}_{0} = 490\quad \text{ and }\quad {y}_{0} = -196
|
solve 5x + 12y = 98.
To find all solutions,
To find non-negative solutions, first consider how to make y positive. Here t = -40 makes y = 4. Trying x, x = 10. So one solution is
|
{x}_{+} = 10\quad \text{ and }{y}_{+} = 5.
|
With t = -39, y is negative. And with t = -41, x is negative. So this is the only possible solution for the actual problem.
We’ve used real numbers without much thought. For the next week and a half, we’ll fill in a few details.
This week will cover topics in rational numbers and hence fractions. For some people, this will be old hat. For others, this is a continuing thorn in their sides.
This presentation will be a bit different than the text’s more typical structure. I hope that this difference may help some who struggle with rationals and fractions by providing reasons for the rules.
A quick aside on the order in which operations can be applied. Working with fractions stress operator precedence.
Operations generally don’t pass through straight lines, whether horizontal for fractions or vertical for absolute value.
Parentheses force an order. Work from the inner outwards.
The general order of precedence between operations:
Within a class, operations proceed from left to right.
Go through a parenthetical clause and compute every exponent, then every multiplication from left to right, and then every addition from left to right.
When in doubt, use parentheses when you write expressions.
Rational numbers are ratios of integers. In a fraction {n\over d}, n is the numerator and d is the denominator. The rational numbers form a set,
|
ℚ = \{{a\over
b}\kern 1.66702pt |\kern 1.66702pt a  J,b J,b  J,b\mathrel{≠}0\}, J,b\mathrel{≠}0\},
|
where J is the set of all
integers. Let 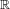 be the set
of all real numbers, then J ⊊ ℚ ⊊
be the set
of all real numbers, then J ⊊ ℚ ⊊ 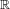 .
The integer on top, a,
is the numerator; the integer on the bottom,
b, is
the denominator.
.
The integer on top, a,
is the numerator; the integer on the bottom,
b, is
the denominator.
Note that this is a very formal construction. We just plop one integer atop another and call it a number. Amazing that it works.
Fractions represent ratios and proportions. When you state that 1 in 10 people are attractive to mosquitos1 , that’s a rational number. We won’t reach probability, where we learn to interpret these ratios correctly, but we will cover basic manipulations of rational numbers.
Two fun points:
Rational arithmetic is based on integer arithmetic. The following properties will be inherited by multiplication and addition for rationals q, r, and s:
 ℚ,
qr
ℚ,
qr  ℚ
ℚ
One homework question is to take the operation definitions below and verify some of these properties.
The following are somewhat formal definitions to show how to construct rationals along strict rules.
We start with multiplication and division. Let
a,b,k,x,y  J, so all
the variables are integers. We will extend these variables to run over the rational
numbers shortly.
J, so all
the variables are integers. We will extend these variables to run over the rational
numbers shortly.
The definition of multiplying fractions:
|
{a\over
b} ⋅{x\over
y} = {ax\over
by}.
|
As an example
|
{3\over
7} ⋅{5\over
2} = {15\over
14}.
|
The definition of a relationship between division and fractions:
|
a∕b = a ⋅{1\over
b} = {a\over
b}\quad \text{so}\quad 8∕2 = a ⋅{1\over
2} = {8\over
2}.
|
We need to be a little careful here. Integer division was defined only when b\mathrel{∣}a, so this expression formally only holds when b\mathrel{∣}a. We relax this restriction later to allow the variables to run over rational numbers.
An important consequence is that
|
a = {a\over
1}
|
for all a.
This leads to very useful technique, expressing 1 as a fraction:
|
1 = k∕k = {k\over
k}
|
for any k\mathrel{≠}0. Remember that in the divisibility form k = 1 ⋅ k + 0, so k\mathrel{∣}k and k∕k = 1.
Next we show what the text calls “the fundamental property of rational numbers”, which is not terribly fundamental. First we show that 1 is the multiplicative identity for rationals by using the fact that 1 is the multiplicative identity for integers,
|
{a\over
b} ⋅ 1 = {a\over
b} ⋅{1\over
1} = {a ⋅ 1\over
b ⋅ 1} = {a\over
b}.
|
Using this fact, we show that {a\over b} = {ak\over bk} for any k\mathrel{≠}0,
|
{a\over
b} = {a\over
b} ⋅ 1 = {a\over
b} ⋅{k\over
k} = {ak\over
bk}.
|
Now we introduce proper fractions. A proper fraction is a rational {a\over b} where the numerator a and denominator b are relatively prime. That is \mathop{gcd}(a,b) = 1 and they share no common factors. Every fraction is equal to some proper fraction. Given \mathop{gcd}(a,b) = d, we can factor out the common divisor,
|
{a\over
b} = {a' ⋅ d\over
b' ⋅ d} = {a'\over
b'} ⋅{d\over
d} = {a'\over
b'}.
|
So for 15 and 35, (15,35) = 5 and
|
{15\over
35} = {3 ⋅ 5\over
7 ⋅ 5} = {3\over
7}.
|
A fraction that is not proper is improper. An improper fraction is a redundant representation, and keeping fractions improper sometimes helps speed operations.
Every rational number with a non-zero numerator has a multiplicative inverse. This uses only the expression for 1 and the relationship between integer division and fractions. Using that a∕a = 1 and commutativity of integer multiplication,
|
1 = (ab)∕(ab) = {ab\over
ab} = {ab\over
ba} = {a\over
b} ⋅ {b\over
a}.
|
So if a\mathrel{≠}0, then {b\over a} is the multiplicative inverse of {a\over b}. As an example,
|
{3\over
5} ⋅{5\over
3} = {15\over
15} = 1.
|
With a multiplicative inverse, we can define division of rationals analogously to the fractional form of division of integers,
|
{a\over
b}∕{x\over
y} = {a\over
b} ⋅{y\over
x} = {ay\over
bx}.
|
For example,
|
{3\over
5}∕{5\over
7} = {3\over
5} ⋅{7\over
5} = {21\over
25}.
|
When adding rational numbers, you must ensure both ratios have the same denominators. This is the same as ensuring measurements are all in the same units; both numerators need measured by the same denominator.
The definition for adding fractions:
|
{a\over
b} + {x\over
y} = {ay\over
by} + {bx\over
by} = {ay + bx\over
by} .
|
Later we will use the least common multiple of b and y to work with a smaller initial denominator. So
|
{1\over
2} + {1\over
3} = {3\over
6} + {2\over
6} = {5\over
6}.
|
Rational numbers have additive identities:
|
{a\over
b} + {0\over
b} = {a + 0\over
b} = {a\over
b}.
|
We prefer there to be only one additive identity. We can use the “fundamental property” above to prove that all additive identities are equal to {0\over 1}:
|
{0\over
b} = {0 ⋅ b\over
1 ⋅ b} = {0\over
1} ⋅{b\over
b} = {0\over
1} ⋅ 1 = {0\over
1}.
|
Given that 1\mathrel{∣}0, {0\over 1} = 0∕1 = 0. So zero is the additive identity for rationals as well as integers.
Like integers, rationals have additive inverses:
|
{a\over
b} + {-a\over
b} = {a + -a\over
b} = {0\over
b} = 0.
|
Given the additive inverse exists, we can define the negation of a rational as
|
-\kern 1.66702pt {a\over
b} = {-a\over
b} ,
|
and then we define subtraction in terms of addition as
|
{a\over
b} -{x\over
y} = {a\over
b} + {-x\over
y} = {ay - bx\over
xy} .
|
So
|
{1\over
2} -{1\over
3} = {3\over
6} + {-2\over
6} = {1\over
6}.
|
We start with some high-level definitions and find the common product rule for comparing fractions.
First, a quick review of integer ordering. We say an integer is negative if it has a negative sign, e.g. -1. An integer is positive if it is neither zero nor negative, or equivalently if the integer is also a counting number. We start an ordering of the integers by saying that a positive i > 0, a negative i < 0, and 0 = 0.
Then we can compare two integers i and j by their difference. There are three cases:
This phrasing may help with the common confusion regarding comparisons and multiplication by negative numbers.
Consider two integers 3 < 5. That 3 < 5 implies 3 - 5 < 0 (and we know it is -2). Now multiply both sides here by -1. If 3 - 5 < 0, that implies 3 - 5 is negative, and in turn - 1 ⋅ (3 - 5) = 5 - 3 = 2 is positive. Thus multiplying both sides by -1 (and hence any negative number) requires reversing the comparison. Here - 1 ⋅ (3 - 5) = 5 - 3 > 0. But by the distributive property, - 1 ⋅ (3 - 5) = (-3) - (-5) as well, so (-3) - (-5) > 0 and - 3 > -5.
Returning to rationals, the integers are a subset, so an order on the rationals should respect the same ordering on the integer subset.
A positive fraction is equal to some fraction where both the numerator and denominator are positive integers. So both the numerator and denominator must have the same sign,
|
{3\over
5},\quad \text{or}\quad {-3\over
-5} = {3\over
5} ⋅{-1\over
-1} = {3\over
5}.
|
A negative fraction is equal to some fraction where the numerator is negative and the denominator is positive. Here the signs must be opposite,
|
{-3\over
5} ,\quad \text{or}\quad {3\over
-5} = {-3\over
5} ⋅{-1\over
-1} = {-3\over
5} .
|
As we saw with the additive identity, a zero fraction is equal to the integer zero and has a zero numerator. The sign of zero does not matter in rational arithmetic (although it may in a computer’s floating-point arithmetic).
Given two rationals r and q, r is strictly less than q, r < q, if q - r is positive. Thus
|
{{q}_{n}\over
{q}_{d}} -{{r}_{n}\over
{r}_{d}} = {{q}_{n}{r}_{d} - {q}_{d}{r}_{n}\over
{q}_{d}{r}_{d}} > 0.
|
We can always move negative signs into the numerator, so we assume that {q}_{d} and {r}_{d} are positive. But remember to convert the fraction into having a positive denominator! Then the above relation
|
{q}_{n}{r}_{d} - {q}_{d}{r}_{n} > 0\quad \text{or, equivalently,}\quad {q}_{n}{r}_{d} > {q}_{d}{r}_{n}.
|
So
|
{{q}_{n}\over
{q}_{d}} > {{r}_{n}\over
{r}_{d}}\quad \text{when}\quad {q}_{n}{r}_{d} > {q}_{d}{r}_{n}.
|
By symmetry, then we can compare two rational numbers by comparing appropriate products.
Consider comparing {1\over 2} and {1\over 3},
|
1 ⋅ 3 > 1 ⋅ 2 ⇒ {1\over
2} > {1\over
3}.
|
And for the negations {-1\over 2} and {-1\over 3} ,
|
-1 ⋅ 3 < -1 ⋅ 2 ⇒ {-1\over
2} < {-1\over
3} .
|
As an example of why you need to force the denominator to be positive, consider {1\over 2} and {-1\over -3}.
|
1 ⋅-3 < -1 ⋅ 2⇏{1\over
2} < {1\over
3}.
|
This is because we are in essence multiplying both sides by the product of their denominators. That product is negative, so we would have to flip the sign. It’s just as easy to remember to make the denominator positive.
So far, the numerator and denominator have been integers. We can loosen the definition slightly and allow complex fractions where the numerator and denominator are rational numbers. We extend the division definition to map complex fractions into fractions with integral numerators and denominators,
|
{{a\over
b}\over
{x\over
y}} = {a\over
b}∕{x\over
y} = {a\over
b} ⋅{y\over
x} = {ay\over
bx}.
|
We could use this definition to show that all the arithmetic operations work as expected on complex fractions.
Working with complex fractions sometimes allows adding fractions without using a massive denominator.
Let L be the least common multiple of b and y. Then b\mathrel{∣}L and y\mathrel{∣}L, so L∕b and L∕y are integers. We can manipulate the addition definition slightly by introducing L,
With 75 =\mathop{ lcm}\nolimits (15,25),
Quite often there is less work in reducing the result into proper form if you use the least common multiple as the denominator.