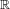Chapter 33
Notes for the tenth week: Irrationals and decimals

Notes also available as PDF.

• exponents, roots, and irrationals
• decimals and percentages
• floating-point arithmetic

exponents, roots, and irrationals

• exponents, rules, etc.
• extending to negative exponents: rationals
• extending to rational exponents leads to roots
• roots to/from exponents

33.1 Real numbers

We won’t define the real numbers. That requires more time than we can allow here. We will simply use the reals, denoted 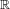, as more than the rationals. This was the state of affairs until around 1872 when Richard Dedekind finally discovered a way to construct real numbers formally.

So the reals fit into our system of sets on the very top,

\text{ natural numbers } ⊊ \text{ whole numbers } ⊊ J ⊊ ℚ ⊊ .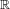

Look up the term “Dedekind cut” for more on actually defining real numbers.

33.2 Exponents and roots

We will cover:

• definition for positive integer exponents,
• rules,
• zero exponents,
• negative exponents, and
• rational exponents and roots.

33.2.1 Positive exponents

We’ve already used positive exponents when discussing the digit representation of numbers:

In general, for any number (integer, rational, or real), the number raised to an integer exponent is defined as:

For example,

Negative numbers have signs that bounce around:

With the symbolic definition, we can show other properties of exponentiation:

In general,

For example,

Or when multiplying numbers raised to powers, we have that exponents add as in

For example,

And numbers raised to powers multiple times multiply exponents as in

For example,

33.2.2 Zero exponent

Consider the following relationship between integer exponents and division:

Reasoning inductively, we suspect that

Using the rule above for adding exponents along with the additive identity property that k + 0 = k, we can deduce that

So for any a\mathrel{≠}0,

Why can’t we define this for a = 0? {0}^{k} = 0 for any integer k > 0. So 0 = {0}^{k} = {0}^{k} ⋅ {0}^{0} does not help to define {0}^{0}; we’re left with 0 = 0 ⋅ {0}^{0}. Because 0 ⋅ x = 0 for any x, {0}^{0} can be anything.

Examples:

33.2.3 Negative exponents

Continuing inductively for a\mathrel{≠}0,

Again, we can use the fact that exponents add to derive this deductively:

and so {a}^{-k} is the multiplicative inverse of {a}^{k}, and we previously showed that to be {1\over { a}^{k}}. We have shown that

for all a\mathrel{≠}0.

For example:

is the inverse of

Also,

is the multiplicative inverse of

And

is the multiplicative inverse of

33.2.4 Rational exponents and roots

So we’ve played with division and exponents. Consider now reasoning inductively using the multiplication rule for exponents:

We call {a}^{{1\over 2} } the square root of a and write \sqrt{a}.

But \sqrt{a} is only defined some of the time. Over integers, there clearly is no integer b such that {b}^{2} = 2, so \sqrt{2} is not defined over the integers and fractional exponents are not closed over integers.

Also, the product of two negative numbers is positive, and the product of two positive numbers is positive, so there is no real number whose square is negative. Hence for real a,

Remember that {(-b)}^{2} = {(-1)}^{2} ⋅ {b}^{2} = {b}^{2}, so the square root may be either positive or negative!

In most circumstances, \sqrt{a} means the positive root, often called the principal square root. When you hit a square-root key or apply a square root in a spreadsheet, you get the principal square root.

Other rationals provide other roots:

is the cube root,

Here, though, {(-a)}^{3} = {(-1)}^{3} ⋅ {a}^{3} = -({a}^{3}), and there is no worry about the sign of the cube root.

Using {({a}^{k})}^{m} = {a}^{km}, we also have

The exponential operator can be defined on more than just the rationals, but we won’t go there. However, remember that I mentioned the rationals are dense in the reals. There is a rational number close

33.2.5 Irrational numbers

There are more reals than rationals. This is a very non-obvious statement. To justify it, we will

• prove that \sqrt{2} is not rational, and
• generalize that proof to other roots.

Remember the table to show that there are as many integers as rationals? You cannot construct one for the reals. I might show that someday. It’s shockingly simple but still a mind-bender. But for now, a few simple examples suffice to make the point.

Theorem: The number \sqrt{2} is not rational.

Theorem: Suppose x and n are positive integers and that \root{n}\of{x} is rational. Then \root{n}\of{x} is an integer.

With decimal expansions, we will see that rational numbers have repeating expansions. Irrational numbers have decimal expansions that never repeat. There are some fascinating properties of the expansions

Irrational numbers come in two kinds, algebraic and transcendental. We won’t go into the difference in detail, but numbers like \sqrt{ 2} are algebraic, and numbers like π and e are transcendental.

33.3 Decimal expansions and percentages

Remember positional notation:

Given negative exponents, we can expand to the right of 1{0}^{0}. General English notation uses a decimal point to separate the integer portion of the number from the rest.

So with the same notation,

Operations work in exactly the same digit-by-digit manner as before. When any position goes over 9, a factor of 10 carries into the next higher power of 10. If any digit becomes negative, a factor of 10 is borrowed frrom the next higher power of 10.

Other languages use a comma to separate the integer from the rest and also use a period to mark off powers of three on the other side, for example

You may see this if you play with “locales” in various software packages. Obviously, this can lead to massive confusion among travellers. (A price of 1.234 is not less than 2 but rather greater than 1000.)

Typical international mathematical and science publications use a period to separate the integer and use a space to break groups of three:

33.3.1 Representing rationals with decimals

What is the part to the right of the decimal point? It often is called the fractional part of the number, giving away that it is a representation of a fraction.

Here we consider the decimal representation of rational numbers {1\over a} for different integers a. We will see that the expansions fall into two categories:

1. some terminate after a few digits, leaving the rest zero; and
2. some repeat a trailing section of digits.

For rational numbers, these are the only two possibilities.

We can find the decimal expansions by long division.

Two simple examples that terminate:

Note that 2\mathrel{∣}10 and 5\mathrel{∣}10, so both expansions terminate immediately with {1\over 2} = .5 and {1\over 5} = .2.

Actually, all fractions with a denominator consisting of powers of 2 and five have terminating expansions. For example,

What if the denominator a in {1\over a} does not divide 10, or a ∤ 10? Then the expansion does not terminate, but it does repeat. If the denominator has no factors of 2 or 5, it repeats immediately.

Examples of repeating decimal expansions:

We write these with a bar over the repeating portion, as in

We say that 0.\overline{3} has a period of 1 and 0.\overline{142857} has a period of 6.

We could write 0.2 = 0.2\overline{0}, but generally we say that this terminates once we reach the repeting zeros.

If the denominator a contains factors of 2 or 5, the repeating portion occurs a number of places after the decimal. For example, consider {1\over 6} = {1\over 2⋅3} and {1\over 45} = {1\over 5⋅9}:

So the decimal representations are

The hard way to determine the period of a repeating fraction

Note that for all non-negative integer k,

These tell us that the expansions have periods of 0, 0, and 1.

For seven,

so the period is of length 7.

For 45,

This is a little more complicated, but the pattern shows that there is one initial digit before hitting a repeating pattern, exactly like the expansion {1\over 45} = 0.0\overline{2}.

In each case, we are looking for the order of 10 modulo the denominator. Finding an integer with a large order modulo another integer is a building block in RSA encryption used in SSL (the https prefix in URLs).

33.3.2 The repeating decimal expansion may not be unique!

One common stumbling block for people is that the repeating decimal expansion is not unique.

Let

Then multiplying n by 10 shifts the decimal over one but does not alter the pattern, so

Given

we can subtract n from the former.

With 9n = 9, we know n = 1. Thus 1 = 0.\overline{9}!

This is a consequence of sums over infinite sequences, a very interesting and useful topic for another course. But this technique is useful for proving that rationals have repeating expansions.

33.3.3 Rationals have terminating or repeating expansions

Theorem: A decimal expansion that repeats (or terminates) represents a rational number.

Theorem: All rational numbers have repeating or terminating decimal expansions.

33.3.4 Therefore, irrationals have non-repeating expansions.

So we know that any repeating or terminating decimal expansion represents a rational, and that all rationals have terminating or repeating decimal expansions.

Thus, we have the following:
Corollary: A number is rational if and only if it has a repeating decimal expansion.

So if there is no repeating portion, the number is irrational. One example,

has an increasing number of zero digits between each one digit. This number is irrational.

It’s beyond our scope to prove that π is irrational, but it is. Thus the digits of π do not repeat.

33.3.5 Percentages as rationals and decimals

Percentage comes from per centile, or part per 100. So a direct numerical equivalent to 85% is

We can expand fractions to include decimals in the numerator and denominator. The decimals are just rationals in another form, and we already explored “complex fractions” with rational numerators and denominators.

So we can express decimal percentages,

Everything else “just works”. To convert a fraction into a percentage, there are two routes. One is to convert the denominator into 100:

Another is to produce the decimal expansion and then multiply that by 100:

Converting a percentage into a proper fraction required dropping the percentage into the numerator and then manipulating it appropriately:

33.4 Fixed and floating-point arithmetic

So far we have considered infinite expansions, ones that are not limited to a set number of digits. Computers (and calculators) cannot store infinite expansions that do not repeat, and those that do require more overhead than they are worth.

Instead, computers round infinite results to have at most a fixed number of significant digits. Operations on these limited representations incur some round-off error, leading to a tension between computing speed and the precision of computed results. One important fact to bear in mind is that precision does not imply accuracy. The following is a very precise but completely in-accurate statement:

First we’ll cover different rounding rules from the perspective of fixed-point arithmetic, or arithmetic using a set number of digits to the right of the decimal plce. Then we’ll explain floating-point arithmetic where the decimal point “floats” through a fixed number of significant digits.

We will not cover the errors in floating-point operations, but we will cover the errors that come from typical binary representation of decimal data.

The points you need to take away from this are the following:

• Using a limited number of digits (or bits) to represent real numbers leads to some inherent, representationall error.
• Representing every-day decimal quantities in binary also incurs some representational error.

Despite the doom-like points above, floating-point arithmetic often provides results that are accurate enough. We won’t be able to cover why this is, but the high-level reasons include:

• using far more digits of precision than initially appear necessary, and
• carrying intermediate results to even higher precision.

33.4.1 Rounding rules

Generally, computer arithmetic can be modelled as computing the exact result and then rounding that exact result into an economical representation.

truncation or rounding to zero

With this rounding method, digits beyond the stored digits are simply dropped.

rounding half-way away from zero

This is the text’s method of “round half up”. A number is rounded to the nearest representable number. In the half-way case, where the digits beyond the number of digits stored are 5000\mathrel{⋯}\kern 1.66702pt , the number is rounded upwards.

rounding half-way to even

This is the preferred method for rounding in general. A number is rounded to the nearest representable number. In the half-way case, where the digits beyond the number of digits stored are 5000\mathrel{⋯}\kern 1.66702pt , the number is rounded so the final stored digit is even.

There are more rounding methods, but these suffice for our discussion. Rounding rules are hugely important in banking and finance, and there are quite a few versions required by different regulations and laws.

Examples of each rounding method above, rounding to two places after the decimal point:

Rounding error is the absolute difference between the exact number and the rounded, stored representation. In the table above, the rounding error in representing {1\over 3} is |{1\over 3} - 0.33| = |{1\over 3} - {33\over 100}| = |{100\over 300} - {99\over 300}| = {1\over 300} = 0.00\overline{3}. Note that here the rounding error is 1% of the exact result. That error is large because we use only two digits.

Note that you cannot round in stages. Consider round-to-nearest-even applied to 0.99455 and rounding to two places after the point:

33.4.2 Floating-point representation

Consider repeatedly dividing by 10 in fixed-point arithmetic that carries two digits beyond the decimal:

So (\kern 1.66702pt (\kern 1.66702pt 1 ÷ 10\kern 1.66702pt ) ÷ 10\kern 1.66702pt ) ÷ 10 evaluates to 0! This phenomenon is called underflow, where a number grows too small to be represented. A similar phenomenon, overflow, occurs when a number becomes too large to be represented. Computer arithmetics differ on how they handle over- and underflow, but generally overflow produces an ∞ symbol and underflow produces 0.

Floating-point arithmetic compensates for this by carrying a fixed number of significant digits rather than a fixed number of fractional digits. The position of the decimal place is carried in an explicit, integer exponent. This allows floating-point numbers to store a wider range and actually makes analysis of the round-off error easier.

In floating-point arithmetic,

This continues until we run out of representable range for the integer exponents. We leave the details of floating-point underflow for another day (if you’re unlucky).

33.4.3 Binary fractional parts

Just as integers can be converted to other bases, fractional parts can be converted as well.

Each position to the right of the point (no longer the decimal point) corresponds to a power of the base. For binary, the typical computer representation,

So a binary fractional part can be expanded with powers of two:

To find a binary expansion, we need to carry out long division in base 2. I won’t ask you to do that.

The important part to recognize is that finite decimal expansions may have infinite, repeating binary expansions! Remember that in decimal, 2\mathrel{∣}10 and 5\mathrel{∣}10, so negative powers of 2 and 5 have terminating decimal expansions. In binary, only 2\mathrel{∣}2, so only powers of 2 have terminating binary expansions.

Numbers you expect to be exact are not. Consider 0.1. Its binary expansion is

A five-bit fixed-point representation would use

The error in representing this with a five-digit fixed-point representation is 0.00625, or over 6%.

In a five-bit floating-point representation,

The error here is less than 0.0024, or less than 0.24%. You can see what floating-point gains here.

Ultimately, though, in a limited binary fractional representation, adding ten dimes does not equal one dollar! This is why often programs slanted towards finance (e.g. spreadsheets) use a form of decimal arithmetic. On current common hardware, decimal arithmetic is implemented in software rather than hardware and is orders of magnitude slower than binary arithmetic.