Chapter 21
Solutions for sixth week’s assignments

Note: These are my approaches to these problems. There are many ways to tackle each.

21.1 Problem set 3.1

Problem 8

Assuming the accounting style and not the calender style, the first number to add is 5 ⋅ 2{0}^{2} + 6 ⋅ 20 + 13 and the second is 11 ⋅ 20 + 8, but we don’t need these forms. We can add Mayan digit by Mayan digit instead. The bottom digit is three bars and six dots, which simplifies to four bars and one dot, or one dot and one dot carried up to the next digit. The next digit is three bars and three dots, where one of those dots is the carry. There are no carries here, so the top digit is just a bar. The final result: One dot in the bottom digit, three bars and three bars in the next digit up, then a single bar in the top-most digit.

Problem 16

24\kern 1.66702pt 872 = \mathbf{2 ⋅ 1{0}^{4} + 4 ⋅ 1{0}^{3} + 8 ⋅ 1{0}^{2} + 7 ⋅ 1{0}^{1} + 2 ⋅ 1{0}^{0}}, 3\kern 1.66702pt 071 = \mathbf{3 ⋅ 1{0}^{3} + 0 ⋅ 1{0}^{2} + 7 ⋅ 1{0}^{1} + 1 ⋅ 1{0}^{0}}

Problem 32

500 + \mathbf{60} + 9 = 569

Problem 34

300 + \mathbf{80} + 5 = 385

Problem 35

2 ⋅ 10 + 18 = 2 ⋅ 10 + 10 + 8 = (2 + 1) ⋅ 10 + 8 = 3 ⋅ 10 + 8 = \mathbf{38}.

21.2 Problem set 3.2

Problem 3

The last digit, the one corresponding to {6}^{0} = 1, is constant down the table. The first digit, the one corresponding to {6}^{1} = 6, is constant across the table. Along each diagonal, both digits increase by one at each step. There are other patterns, but these are some of the most obvious.

Problem 4

The next two rows:

60	61	62	63	64	65
70	71	72	73	74	75

Problem 5

• 41{3}_{5} = 4 ⋅ {5}^{2} + 1 ⋅ 5 + 3 = 108
• 200{4}_{5} = 2 ⋅ {5}^{3} + 4 = 254
• 1{0}_{5} = 1 ⋅ 5 = 5
• 10{0}_{5} = 1 ⋅ {5}^{2} = 25
• 100{0}_{5} = 1 ⋅ {5}^{3} = 125
• 213{4}_{5} = 2 ⋅ {5}^{3} + 1 ⋅ {5}^{2} + 3 ⋅ 5 + 4 = 294

Problem 6

• 41{3}_{6} = 4 ⋅ {6}^{2} + 1 ⋅ 6 + 3 = 153
• 200{4}_{6} = 2 ⋅ {6}^{3} + 4 = 436
• 1{0}_{6} = 1 ⋅ 6 = 6
• 10{0}_{6} = 1 ⋅ {6}^{2} = 36
• 100{0}_{6} = 1 ⋅ {6}^{3} = 216
• 213{4}_{6} = 2 ⋅ {6}^{3} + 1 ⋅ {6}^{2} + 3 ⋅ 6 + 4 = 490

Problem 8

• 362 = 242{2}_{5}
• 27 = 10{2}_{5}
• 5 = 1{0}_{5}
• 25 = 10{0}_{5}

Problem 11

• {2}^{0} =	1
  {2}^{1} =	2
  {2}^{2} =	4
  {2}^{3} =	8
  {2}^{4} =	16
  {2}^{5} =	32
  {2}^{6} =	64
  {2}^{7} =	128
  {2}^{8} =	256
  {2}^{9} =	512
  {2}^{10} =	1024

• • 110{1}_{2} = 13
  • 11{1}_{2} = 7
  • 100{0}_{2} = 8
  • 1010{1}_{2} = 21
• • 24 = 1100{0}_{2}
  • 18 = 1001{0}_{2}
  • 2 = 1{0}_{2}
  • 8 = 100{0}_{2}

• 0 =	{0}_{2} =	0000{0}_{2}
  1 =	{1}_{2} =	0000{1}_{2}
  2 =	1{0}_{2} =	0001{0}_{2}
  3 =	1{1}_{2} =	0001{1}_{2}
  4 =	10{0}_{2} =	0010{0}_{2}
  5 =	10{1}_{2} =	0010{1}_{2}
  6 =	11{0}_{2} =	0011{0}_{2}
  7 =	11{1}_{2} =	0011{1}_{2}
  8 =	100{0}_{2} =	0100{0}_{2}
  9 =	100{1}_{2} =	0100{1}_{2}
  10 =	101{0}_{2} =	0101{0}_{2}
  11 =	101{1}_{2} =	0101{1}_{2}
  12 =	110{0}_{2} =	0110{0}_{2}
  13 =	110{1}_{2} =	0110{1}_{2}
  14 =	111{0}_{2} =	0111{0}_{2}
  15 =	111{1}_{2} =	0111{1}_{2}
  16 =	1000{0}_{2} =	1000{0}_{2}
  17 =	1000{1}_{2} =	1000{1}_{2}
  18 =	1001{0}_{2} =	1001{0}_{2}
  19 =	1001{1}_{2} =	1001{1}_{2}
  20 =	1010{0}_{2} =	1010{0}_{2}
  21 =	1010{1}_{2} =	1010{1}_{2}
  22 =	1011{0}_{2} =	1011{0}_{2}
  23 =	1011{1}_{2} =	1011{1}_{2}
  24 =	1100{0}_{2} =	1100{0}_{2}
  25 =	1100{1}_{2} =	1100{1}_{2}
  26 =	1101{0}_{2} =	1101{0}_{2}
  27 =	1101{1}_{2} =	1101{1}_{2}
  28 =	1110{0}_{2} =	1110{0}_{2}
  29 =	1110{1}_{2} =	1110{1}_{2}
  30 =	1111{0}_{2} =	1111{0}_{2}
  31 =	1111{1}_{2} =	1111{1}_{2}

  One of the more important patterns to see is how the digits repeat once padded to the left by zeros. The units (or right-most) digit alternates 0,1,0,1,\mathop{\mathop{…}}. The next alternates in pairs, 0,0,1,1,0,0,1,1,\mathop{\mathop{…}}. The next in groups of four, the next in groups of eight, and so forth.

• In one sentence: They’re the same thing.

Problem 20

• Base two digits take two values, so a three-digit numeral may take one of 2 ⋅ 2 ⋅ 2 = 8 values.
• The problem is the same, so there are eight possible subsets. This is how we described the power-set operation, and 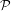(A) = {2}^{|A|} for any set A.
• The same argument or reference provides {2}^{4} = 16 subsets.
• The general result is {2}^{n}.

21.3 Problem set 3.3

Problem 10

In order, the steps are associativity, associativity, commutativity, associativity, associativity, and distributivity of addition over multiplication.

Problem 12

+	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

Problem 20

• Here, 1 + 4 = 0 in the units digit, so the base must be 5.
• 2 + 4 = 0 two places over, and 3 + 1 = 4 without a carry before it, so the base must be 6.
• There are no carries in the sum at all, so the base is indeterminant. The base can be any integer at least 7 because the largest digit that appears is 6.
• 3 + 1 = 0, but the before it 4 + 4 = 4 must carry and itself be afffected by a carry. The base is 5.
• Swap the subtraction around, so 236 + 254 = 523. If 6 + 4 = 3 plus a carry, the base is 7.
• 247 + 254 = 523. With 7 + 4 = 3 plus a carry, the base is 8.
• 28\text{E} + 254 = 523. Now \text{E} + 4 = 3 plus a carry, so the base is \text{E} + 1 = \text{F} or 15.

21.4 Problem set 3.4

Problem 5

In order of blanks, distributivity of addition over multiplication, commutativity of multiplication, associativity of addition, and distributivity of addition over multiplication.

Problem 17

• 	3	7	4
  0	0/6	1/4	0/8	2
  8	0/3	0/7	0/4	1
  0	1/5	3/5	2/0	5
  	4	1	0

  So 374 ⋅ 215 = 80410.

• The lattice algorithm works digit by digit. This is the same as the method in class but using diagonals rather than writing in columns.
• I would hope so, but it hasn’t so far. Working with a set of Napier’s bones could help. Those are physical rods you use to build these columns.

Problem 19

• The Egyptian algorithm essentially converts the multiplier to binary. Then it doubles the multiplicand at each step and adds the intermediate product to the result if the corresponding bit of the multiplier is 1.
• I have never heard of the “duplation” algorithm (perhaps duplication?). But one way to write out the method is to convert 24 to binary, 24 = 1100{0}_{2}. Now start with an accumulator of 0:

  bit of 17	doubling of 71	accumulator
  		0
  0	71	0
  0	142	0
  0	284	0
  1	568	568
  1	1136	1704

  So 71 ⋅ 24 = 1704.

Problem 33

Problem	Actual answer	Calculator’s answer
8 × 3	24	34
9 × 5	45	55
4 × 2	8	18
8 × 4	32	42
a × b	x - 10	x
9 × 6	64 - 10 = 54	64

When the decimal logic was done outside a chip (the early 80s), this type of failure could happen from a simple short-circuit. Now it’s highly doubtful; a failure like this would require massive trauma to the chip, leading to general failure.